Randomisierte Algorithmen - 6. Graph

Randomisierte Algorithmen
Randomisierte Algorithmen
6. Graph-Algorithmen
Thomas Worsch
Fakultät für Informatik
Karlsruher Institut für Technologie
Wintersemester 2016/2017
1 / 81
Graph-Algorithmen
Überblick
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
2 / 81
Graph-Algorithmen
Einleitung
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
3 / 81
Graph-Algorithmen
Einleitung
6.1 Definition (Multigraph)
I
ungerichteter Multigraph (V , E, v) mit
I
I
I
Knotenmenge V der Größe n = |V |
Kantenmenge E der Größe m = |E|
Abbildung v : E → {{x, y} | x, y ∈ V }
I
Es sind Mehrfachkanten möglich.
I
In diesem Kapitel:
keine Schlingen, also ∀e ∈ E : |v(e)| = 2.
4 / 81
Graph-Algorithmen
Einleitung
6.3 Repräsentation von Multigraphen
I
«Adjazenzmatrix» A der Größe n × n
Eintrag A[x,
y]: Anxahl
Kanten zwischen x und y:
A[x, y] = v −1 ({x, y})
I
außerdem nützlich: Vektor M der Größe n:
Eintrag M[x] gibt an, wieviele Kanten von x wegführen:
Í
M[x] = y A[x, y]
5 / 81
Graph-Algorithmen
Minimale Schnitte
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
6 / 81
Graph-Algorithmen
Minimale Schnitte
6.4 Definition Schnitte
I
Ein Schnitt in einem Multigraphen ist
eine Partitionierung V = C ∪ C̄.
I
Größe des Schnittes ist
die Anzahl der Kanten {x, y} mit x ∈ C und y ∈ C̄.
7 / 81
Graph-Algorithmen
Minimale Schnitte
MINCUT
I
Probleminstanz: ein Graph G
I
Frage: Wie groß sind die minimalen Schnitte von G?
I
beste bekannte deterministische Algorithmen brauchen
Laufzeit O(mn + n2 log n) ⊆ O(n3 )
I
I
für planare Graphen reicht O(n(log n)2 )
randomisiert?
8 / 81
Graph-Algorithmen
Minimale Schnitte
6.5 Lemma
Wenn die Größe der minimalen Schnitte k ist, dann
I
hat jeder Knoten mindestens Grad k
I
ist die Anzahl Kanten m ≥ nk/2
9 / 81
Graph-Algorithmen
Minimale Schnitte
6.6 Beweis
I
Wäre anderenfalls deg(x) < k,
I
dann hätte der Schnitt mit C = {x } eine Größe echt kleiner k.
10 / 81
Graph-Algorithmen
Minimale Schnitte
6.7 Definition Kontraktion
I
I
In Multigraph G seien Knoten x und y durch eine Kante e mit
v(e) = {x, y} verbunden.
G/e entsteht durch Kontraktion der Kante e:
I
I
Knotenmenge V 0 = (V r {x, y}) ∪ {z}, wobei z neu ist.
Kantenmenge E 0 ergibt sich aus E, indem
I
I
I
alle Kanten zwischen x und y entfernt werden,
jede Kante zwischen v ∈ V r {x, y} und x oder y ersetzen durch
Kante zwischen v und z
alle anderen Kanten von G übernehmen
11 / 81
Graph-Algorithmen
Minimale Schnitte
6.8 Beispiel
e1
v
x
e01
e
e2
v
z
e02
y
Es können Mehrfachkanten entstehen.
12 / 81
Graph-Algorithmen
Minimale Schnitte
6.9 Lemma
Minimale Schnitte von G/e sind



 mindestens? 



genauso?
so groß

 höchstens? 



wie minimale Schnitte von G.
13 / 81
Graph-Algorithmen
Minimale Schnitte
6.9 Lemma
Minimale Schnitte von G/e sind



 mindestens! 



genauso?
so groß

 höchstens? 



wie minimale Schnitte von G.
13 / 81
Graph-Algorithmen
Minimale Schnitte
6.10 Beweis
I
Betrachte minimalen Schnitt (K, K̄) von G/e.
I
Seine Größe sei k.
I
O. B. d. A. seien die Endknoten x und y von e in K.
I
Indem man diese beiden Knoten «aus der Kontraktion auspackt»
und in der gleichen Partition belässt, erhält man einen Schnitt von
G, dessen Größe ebenfalls k ist.
I
Also haben die minimalen Schnitte von G höchstens Größe k.
14 / 81
Graph-Algorithmen
Minimale Schnitte
6.11 Algorithmus
I
I
Sei G Multigraph mit Kante e zwischen x und y > x.
Wie in 6.3 vereinbart, sei
I
I
I
I
A «Adjazenzmatrix» Í
M Vektor mit M[x] = y A[x, y]
n, m Variablen für Knoten- bzw. Kantenzahl
Die Datenstrukturen für G/e lassen sich wie folgt in Linearzeit
berechnen:
15 / 81
Graph-Algorithmen
Minimale Schnitte
6.11 Algorithmus (2a)
proc graph ← Kontraktion(graph G, edge e)
x ← min(v(e))
y ← max(v(e))
hy , x da G schlingenfreii
hIdee: benutze Zeile/Spalte «x für z»i
h
und Zeile/Spalte «y für n»i
z ←x
hAktualisierung der Kantenzahleni
m ← m − A[x, y]
M[z] ← M[x] + M[y] − 2 · A[x, y]
M[y] ← M[n]
16 / 81
Graph-Algorithmen
Minimale Schnitte
6.11 Algorithmus (2b)
hAktualisierung von Zeile/Spalte z:i
A[z, ·] ← A[x, ·] + A[y, ·]
A[·, z] ← A[·, x] + A[·, y]
A[z, z] ← 0
hAktualisierung von Zeile/Spalte y: i
A[y, ·] ← A[n, ·]
A[·, y] ← A[·, n]
hdie bisherige Zeile n ist nun bedeutungslosi
hAktualisierung der Knotenzahli
n ←n−1
return hGraph, der zu den neuen Datenstrukturen gehörti
17 / 81
Graph-Algorithmen
Minimale Schnitte
6.12 Erster randomisierter Algorithmus
18 / 81
Graph-Algorithmen
Minimale Schnitte
6.12 Erster randomisierter Algorithmus
Iterierte Kontraktion
18 / 81
Graph-Algorithmen
Minimale Schnitte
6.12 Erster randomisierter Algorithmus
Iterierte Kontraktion
hEingabe: ein Multigraph G(V , E)i
hAusgabe: ein Schnitt (C, C̄)i
H ←G
while (H hat mehr als 2 Knoten) do
e ← hzufällig gleichverteilt gewählte Kante von H i
H ← Kontraktion(H , e)
od
(C, C̄) ← hdie Knotenmengen von G,i
hdie den Knoten von H entsprecheni
18 / 81
Graph-Algorithmen
Minimale Schnitte
6.13 Satz
Algorithmus 6.12 kann so implementiert werden, dass die Laufzeit in
O(n2 ) ist.
19 / 81
Graph-Algorithmen
Minimale Schnitte
6.14 Beweis
I
Jeder Aufruf von Kontraktion benötigt Laufzeit O(n).
I
Bei jedem Schleifendurchlauf wird die Anzahl der Knoten von H
um 1 erniedrigt, d. h. es gibt n − 2 solche Durchläufe.
Es bleibt zu implementieren:
I
1. zufällige gleichverteilte Auswahl einer Kante des Multigraphen
2. Beschaffung der Mengen C und C̄
20 / 81
Graph-Algorithmen
Minimale Schnitte
6.14 Beweis (2)
1. Zufällige Kantenwahl:
21 / 81
Graph-Algorithmen
Minimale Schnitte
6.14 Beweis (2)
1. Zufällige Kantenwahl:
i ← random(1, 2m) hNB: jede Kante unten zweimal gezählt!i
x ← 0; s ← 0
while s < i do
x ←x +1
s ← s + M[x]
od
i ← i − (s − M[x])
y ← 0; s ← 0
while s < i do
y ←y+1
s ← s + A[x, y]
od
hWähle Kante zwischen x und yi
21 / 81
Graph-Algorithmen
Minimale Schnitte
6.14 Beweis (3)
2. Beschaffung von C und C̄:
I
I
I
I
weitere Datenstruktur in der Prozedur Kontraktion
boolesche Matrix Q mit so vielen Zeilen und Spalten wie der
ursprüngliche Graph G Knoten hat.
Q[x, y] = 1: Knoten mit Ursprungsnummern x und y wurden
kontrahiert.
Initialisierung: Einheitsmatrix.
I
Q[x, ·] ← Q[x, ·] ∨ Q[y, ·]
Q[y, ·] ← Q[n, ·]
I
Am Ende nur noch zwei Knoten:
I
I
C z. B. durch 1-Einträge in Zeile 1 von Q gegeben
C̄ z. B. durch 0-Einträge in Zeile 1 von Q gegeben
22 / 81
Graph-Algorithmen
Minimale Schnitte
6.15 Satz
Algorithmus 6.12 findet einen minimalen Schnitt mit einer



 ziemlich groß? 



mittel?
ist.
Wahrscheinlichkeit, die

 ziemlich klein? 



23 / 81
Graph-Algorithmen
Minimale Schnitte
6.15 Satz
Algorithmus 6.12 findet einen minimalen Schnitt mit einer



 ziemlich groß? 



mittel?
Wahrscheinlichkeit, die
ist.

 in Ω(n−2 ) 



23 / 81
Graph-Algorithmen
Minimale Schnitte
6.16 Beweis
in 3 Schritten
1. Es sei (C, C̄) irgendein Schnitt. Behauptung:
Algorithmus 6.12 liefert diesen Schnitt als Ergebnis gdw
keine seiner Kanten kontrahiert wird.
I
I
I
sei e eine am Ende noch vorhandene Kante
ursprünglich zwischen x und y
also etwa x ∈ C und y ∈ C̄
wäre e kontrahiert worden, müssten am Ende
x und y zum gleichen Knoten von H gehören
24 / 81
Graph-Algorithmen
Minimale Schnitte
6.16 Beweis (2)
2. Es sei (K, K̄) ein minimaler Schnitt von G der Größe k.
I
I
I
Nach i − 1 Schleifendurchläufen sei noch keine Kante dieses
Schnittes kontrahiert worden.
dann ist (K, K̄) ein Schnitt des dann erhaltenen Graphen Hi−1 und
wegen Lemma 6.9 auch ein minimaler
Also enthält Hi−1 noch mindestens (n − i + 1)k/2 Kanten.
Folglich:
I
I
Wahrscheinlichkeit, dass als nächstes eine der k Kanten, die zum
Schnitt K gehören, kontrahiert wird, höchstens 2/(n − i + 1);
Wahrscheinlichkeit, dass keine dieser Kanten kontrahiert wird,
mindestens 1 − 2/(n − i + 1).
25 / 81
Graph-Algorithmen
Minimale Schnitte
6.16 Beweis (3)
3. Die Wahrscheinlichkeit, dass in keinem der Schritte eine der
Kanten des Schnittes K kontrahiert wird, ist daher mindestens
În−2
n−2 Ö
(n − i − 1)
2
1−
= Îi=1
n−2
n
−
i
+
1
i=1 (n − i + 1)
i=1
=
(n − 2)!
n!/2!
=
(n − 2)!2!
n!
>
2
1
∈ Ω( 2 )
2
n
n
26 / 81
Graph-Algorithmen
Minimale Schnitte
Bemerkung
I
Die Nicht-Fehler-Wahrscheinlichkeit von 1/n2 in Satz 6.15 ist klein.
I
Der kleinste von k = n2 /2 Schnitten ist mit W.keit 1 − 1/e minimal:
2
1− 2
n
n 2 /2
<
1
e
Weitere Rechnung zeigt: k ∈ Ω(n2 ) erzwungen.
I
Gesamtlaufzeit: Θ(n4 )
im Gegensatz zu O(n3 ) im Deterministischen
I
Problem: Bei kleinen Graphen werden zu oft «aus Versehen»
Kanten eines minimalen Schnittes kontrahiert.
I
Besser: randomisiert auf t Knoten kontrahieren,
Rest deterministisch
27 / 81
Graph-Algorithmen
Minimale Schnitte
6.17 Algorithmus
proc graph ← IterContract(graph G, int t)
hEingabe: ein Multigraph G(V , E, v) undi
h
Endzahl t von Knoteni
hAusgabe: ein kontrahierter Graph H i
H ←G
while (H hat mehr als t Knoten) do
e ← hzufällig gleichverteilt gewählte Kante von H i
H ← Kontraktion(H , e)
od
return H
28 / 81
Graph-Algorithmen
Minimale Schnitte
6.18 Lemma
Die Wahrscheinlichkeit, dass bei Algorithmus 6.17 im Ergebnis H noch
ein minimaler Schnitt des ursprünglichen Graphen «noch vorhanden»
ist, ist mindestens
t n
/
.
2 2
29 / 81
Graph-Algorithmen
Minimale Schnitte
6.19 Beweis
Abschätzung analog wie in Beweis 6.16:
În−t
n−t Ö
(n − i − 1)
2
1−
= Îi=1
n−t
n −i +1
i=1 (n − i + 1)
i=1
=
=
În−t −2
i=1 (n − i − 1)t(t − 1)
În−t
n(n − 1) i=3 (n − i + 1)
t(t − 1)
n(n − 1)
t n
=
/
∈ Ω((t/n)2 )
2 2
30 / 81
Graph-Algorithmen
Minimale Schnitte
6.20 Algorithmus
proc cut ← IterContractDetMinCut(graph G, int t)
hEingabe: ein Multigraph G(V , E, v) undi
h
eine Knotenzahl ti
hAusgabe: ein Schnitt von Gi
C ← hein trivialer Schnitti
for i ← 1 to n2 /t 2 do
H ← IterContract(G, t)
D ← DetMinCut(H )
C ← min(C, D)
od
return C
31 / 81
Graph-Algorithmen
Minimale Schnitte
6.21 Lemma
Wählt man in Algorithmus 6.20 t = n2/3, dann ist die Laufzeit in O(n8/3 )
und die Wahrscheinlichkeit, einen minimalen Schnitt von G zu erhalten
mindestens 1 − 1/e.
32 / 81
Graph-Algorithmen
Minimale Schnitte
6.22 Beweis
I
Zeitbedarf ist kleiner gleich
n2
n4
2
3
·
(n
+
t
)
=
+ n 2t .
t2
t2
I
Für gewähltes t beide Summanden größenordungsmäßig in
O(n8/3 ).
I
Fehlerwahrscheinlichkeit höchstens
t2
1− 2
n
n 2 /t 2
<
1
.
e
33 / 81
Graph-Algorithmen
Minimale Schnitte
6.23 Algorithmus
proc cut ← FastCut(graph G)
hEingabe: ein Multigraph G(V , E)i
hAusgabe: ein Schnitt Ci
if (|V | ≤ 6) then
C ← hminimaler Schnitt, deterministisch ermittelti
else
fi
34 / 81
Graph-Algorithmen
Minimale Schnitte
6.23 Algorithmus
proc cut ← FastCut(graph G)
hEingabe: ein Multigraph G(V , E)i
hAusgabe: ein Schnitt Ci
if (|V | ≤ 6) then
C ← hminimaler Schnitt, deterministisch ermittelti
else
√
t ← d1 + n/ 2e
H1 ← IterContract(G, t)
H2 ← IterContract(G, t)
C1 ← FastCut(H1 )
C2 ← FastCut(H2 )
C ← min(C1, C2 )
fi
34 / 81
Graph-Algorithmen
Minimale Schnitte
6.24 Satz
Algorithmus 6.23 hat Laufzeit O(n2 log n).
35 / 81
Graph-Algorithmen
Minimale Schnitte
6.25 Beweis
I
Maximale Rekursionstiefe: Θ(log n).
I
Beide Aufrufe von IterContract benötigen eine Zeit in O(n2 ).
I
Also ist der Gesamtzeitbedarf T (n) für Eingabegraphen mit n
Knoten
l
√ m
T (n) = 2 · T 1 + n/ 2 + O(n2 ) .
I
Hieraus ergibt sich T (n) ∈ O(n2 log n).
36 / 81
Graph-Algorithmen
Minimale Schnitte
6.26 Satz
Algorithmus 6.23 liefert mit Wahrscheinlichkeit in Ω(1/log n) minimalen
Schnitt.
37 / 81
Graph-Algorithmen
Minimale Schnitte
6.27 Beweis
I
G Eingabegraph mit minimalen Schnitten der Größe k
I
Ein solcher Schnitt habe eine Reihe rekursiver Aufrufen von
FastCut bis zu einer Stelle «überlebt».
I
Der dann erreichte Graph heiße H .
I
Durch Aufrufe von IterContract resultieren Graphen H1 und H2.
Der Aufruf für H wird als Ergebnis einen minimalen Schnitt für G
liefern, falls für ein Hi gilt:
I
1. Der Schnitt überlebt die Kontraktionen zur Konstruktion von Hi .
2. FastCut(Hi ) findet einen minimalen Schnitt in Hi .
38 / 81
Graph-Algorithmen
Minimale Schnitte
6.27 Beweis (2)
Die Wahrscheinlichkeit für Punkt 1 ist nach Lemma 6.17 mindestens
√
√
√
√
d1 + t/ 2e(d1 + t/ 2e − 1) t/ 2 · t/ 2 1 t 2
1
≥
≥
≥ .
t(t − 1)
t(t − 1)
2 t(t − 1) 2
39 / 81
Graph-Algorithmen
Minimale Schnitte
6.27 Beweis (3)
Zu Punkt 2.:
I
Interessieren uns für untere Schranke p(r ) der Wahrscheinlichkeit,
dass FastCut r Niveaus über dem Rekursionsabbruch einen
minimalen Schnitt findet.
Z.B. so: p(0) = 1 und
2
p(r )2
1
p(r + 1) = 1 − 1 − · p(r ) = p(r ) −
2
4
I
Einsetzen von q(r ) = 4/p(r ) − 1 bzw. p(r ) = 4/(q(r ) + 1) ergibt
I
4q(r )
4
4
4
=
−
=
2
q(r + 1) + 1 q(r ) + 1 (q(r ) + 1)
(q(r ) + 1)2
I
und weiter q(r + 1) = q(r ) + 1 +
1
q(r ) .
40 / 81
Graph-Algorithmen
Minimale Schnitte
6.27 Beweis (4)
I
Induktion: Für alle r gilt:
r < q(r ) < r + 3 + Hr −1
I
I
Offensichtlich ist q(0) = 3 und r < q(r ) für alle r .
Weiter:
r + 1 < q(r ) + 1 < q(r + 1) = q(r ) + 1 +
1
q(r )
< r + 3 + Hr −1 + 1 +
= (r + 1) + 3 + Hr
I
I
I
1
r
Daher ist q(r ) ∈ r + O(log r ) und folglich p(r ) ∈ Ω(1/r ).
Für Ausgangsgraphen mit n Knoten ist die Rekursionstiefe Θ(log n)
folglich gesuchte Wahrscheinlichkeit Ω(1/log n).
41 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
Problemstellung
Ein deterministischer Algorithmus für MST
F -leichte und F -schwere Kanten
Ein randomisierter MSF-Algorithmus
42 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Problemstellung
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
Problemstellung
Ein deterministischer Algorithmus für MST
F -leichte und F -schwere Kanten
Ein randomisierter MSF-Algorithmus
43 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Problemstellung
Problemstellung
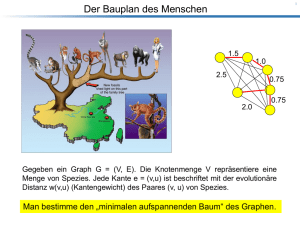
Gegeben: Graph G = (V , E)
I zusammenhängend, ungerichtet
I Kanten e mit reellen Zahlen w(e) gewichtet
Gesucht:
minimaler aufspannender Baum (minimum spanning tree, MST), d. h.
I Teilgraph von G, der
I Baum ist,
I G aufspannt und
I unter allen solchen Bäumen minimales Gewicht hat.
Falls G nicht zusammenhängend, existiert nur ein minimaler
aufspannender Wald (minimum spanning forest, MSF).
44 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Problemstellung
Allgemeine Annahme
O. B. d. A. seien alle Kantengewichte paarweise verschieden.
45 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
Problemstellung
Ein deterministischer Algorithmus für MST
F -leichte und F -schwere Kanten
Ein randomisierter MSF-Algorithmus
46 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Lemma
Jede lokal minimale Kante gehört zu einem MST von G.
47 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Beweis
I
e = {x, y} lokal minimale Kante eines Knotens x.
I
T 0 ein aufspannender Baum von G, der nicht e enthalte.
Zeige: T 0 hat nicht minimales Gewicht.
lautes Nachdenken an der Tafel
48 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Beweis
I
e = {x, y} lokal minimale Kante eines Knotens x.
I
T 0 ein aufspannender Baum von G, der nicht e enthalte.
Zeige: T 0 hat nicht minimales Gewicht.
I
Sei e 0 die Kante von T 0,
I
I
I
I
die von x wegführt und
in T 0 auf dem kürzesten Weg von x nach y liegt.
betrachte T = T 0 − e 0 + e
Behauptungen
1. w(T ) < w(T 0).
2. T spannt G auf.
3. T ist ein Baum.
48 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Korollar
Die lokal minimalen Kanten eines Graphen bilden ein Wald.
49 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Borůvka-Phase
Algorithmus, der folgendes leistet:
1. berechne Menge L(G) aller lokal minimalen Kanten von G
2. berechne den kontrahierten Graphen B(G) = G/L(G)
I
entstünden Mehrfachkanten,
wird nur die leichteste Einzelkante behalten
50 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Lemma
Eine Borůvka-Phase kann man in Zeit O(m + n) implementieren.
Beweis: Übung.
51 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Lemma
Durch eine Borůvka-Phase wird die Anzahl der Knoten um mindestens
die Hälfte reduziert.
52 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Beweis
I
jede Kante für höchstens zwei Knoten lokal minimal
I
also werden in einer Borůvka-Phase mindestens n/2 Kanten
entfernt
I
Mit jeder entfernten Kante wird auch ein Knoten entfernt.
53 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Lemma
Für jeden Graphen G gilt:
Die Kanten in L(G) und die Kanten eines MST von B(G) bilden
zusammen einen MST von G.
54 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Beweis
I
I
I
I
I
Jeder aufspannende Baum T von G, der L(G) «enthält», induziert
einen aufspannenden Baum T 0 von B(G) mit
w(T 0) = w(T ) − w(L(G)).
Jeder aufspannde Baum T 0 von B(G) induziert einen
aufspannenden Baum T¯0 von G, der L(G) «enthält»,
mit w(T ) = w(T 0) + w(L(G)).
Sei T minimaler aufspannender Baum von G und
B(T ) der zugehörige aufspannende Baum von B(G).
Wäre B(T ) nicht minimal für B(G), sondern etwa T 0,
so hätte der dadurch induzierte aufspannende Baum T¯0 von G nur
Gewicht w(T¯0) = w(T 0) + w(L(G)) < w(B(T )) + w(L(G)) = w(T )
im Widerspruch zur Minimalität von T .
55 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Korollar
Wenn alle Kantengewichte paarweise verschieden sind, ist der MST
eindeutig.
56 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Borůvkas MST-Algorithmus
I
Borůvka-Phasen bis nur noch 1 Knoten im Graph
I
führe Buch, welche Kanten jeweils kontrahiert werden
I
vorangegangene Lemmata: klar, welche Kanten MST bilden
57 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Lemma
Borůvkas MST-Algorithmus benötigt O(m log n) Zeit.
58 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Beweis
I
O(log n) viele Phasen,
I
von denen jede O(m + n) Zeit benötigt
I
In zusammenhängenden Graphen ist n ∈ O(m).
59 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Andere deterministische Algorithmen
Bernard Chazelle
A Minimum Spanning Tree Algorithm with Inverse-Ackermann
Type Complexity
Journal of the ACM, 47:1028–1047, 2000.
I Laufzeit O(mα(m, n))
I mit α(m, n) = min{i ≥ 1 : A(i, bm/nc) ≥ log n}
2
60 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Andere deterministische Algorithmen
Bernard Chazelle
A Minimum Spanning Tree Algorithm with Inverse-Ackermann
Type Complexity
Journal of the ACM, 47:1028–1047, 2000.
I Laufzeit O(mα(m, n))
I mit α(m, n) = min{i ≥ 1 : A(i, bm/nc) ≥ log n}
2
Seth Pettie, Vijaya Ramachandran
An optimal minimum spanning tree algorithm
Journal of the ACM, 49:16–34, 2002.
60 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein deterministischer Algorithmus für MST
Andere deterministische Algorithmen
Bernard Chazelle
A Minimum Spanning Tree Algorithm with Inverse-Ackermann
Type Complexity
Journal of the ACM, 47:1028–1047, 2000.
I Laufzeit O(mα(m, n))
I mit α(m, n) = min{i ≥ 1 : A(i, bm/nc) ≥ log n}
2
Seth Pettie, Vijaya Ramachandran
An optimal minimum spanning tree algorithm
Journal of the ACM, 49:16–34, 2002.
«Although our time bound is optimal,
the exact function describing it is not known at present.»
60 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
Problemstellung
Ein deterministischer Algorithmus für MST
F -leichte und F -schwere Kanten
Ein randomisierter MSF-Algorithmus
61 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Definition
I
sei F ein Wald in G
I
v1 und v2 zwei Knoten von G und
I
P(v1, v2 ) die Menge der Kanten des kürzesten Pfades in F von v1
nach v2 (oder P = ∅)
I
Definiere
WF (v1, v2 ) =
(beliebig, nicht notwendig MSF)


max{w(e) | e ∈ P(v1, v2 )}





∞

falls v1, v2 im
gleichen Baum
sonst
I
Kante e = {v1, v2 } heißt F -schwer, falls w(e) > WF (v1, v2 ) ist, und
I
sie heißt F -leicht, falls w(e) ≤ WF (v1, v2 ).
62 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Lemma
I
Es sei
I
I
F ein beliebiger(!) Wald von G und
e = {v1 , v2 } eine Kante in G.
I
Wenn e F -schwer, dann gehört e nicht zum MST von G.
I
äquivalent:
Wenn eine Kante zum MST gehört, dann ist sie F -leicht.
I
I
wohlgemerkt für beliebigen Wald F
äquivalent:
Die schwerste Kante eines Kreises gehört nie zum MST.
63 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Beweis
I
Kante e = {v1, v2 } sei F -schwer und
I
es bezeichne P den Pfad von v1 nach v2, dessen Kanten alle leichter
sind als die Kante e selbst.
I
Bei Bestimmung des MST mit Borůvkas Algorithmus
I
wird e nie lokal minimale Kante von v1 oder v2 sein, sondern
immer eine der Kanten von P.
I
Also wird e auch nie zum (eindeutigen) MST hinzugenommen.
64 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Lemma
Ein aufspannender Baum T eines Graphen G hat minimales Gewicht,
wenn die einzigen T -leichten Kanten in G die Kanten von T sind.
65 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Beweis
I
Wenn die einzigen T -leichten Kanten in G die Kanten von T sind,
I
dann sind alle Kanten, die nicht zu T gehören T -schwer.
I
Also gehören sie also sicher nicht zum MST von G.
I
Also besteht der MST nur aus Kanten, die zu T gehören.
I
Von ihnen kann man aber auch keine weglassen, da es dann kein
aufspannender Baum von G mehr ist.
66 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
F -leichte und F -schwere Kanten
Satz (Dixon (1992), King (1997))
Zu einem Graphen G und einem Wald F in G kann man alle F -schweren
Kanten von G in Zeit O(m + n) finden.
Beweis: nicht leicht.
Wir werden den Satz einfach verwenden.
67 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Überblick
Einleitung
Minimale Schnitte
Minimale aufspannende Bäume
Problemstellung
Ein deterministischer Algorithmus für MST
F -leichte und F -schwere Kanten
Ein randomisierter MSF-Algorithmus
68 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Zufällige Teilgraphen
RandomSample(G, p) sei eine Funktion, die
I
einen Graphen G 0 mit den gleichen Knoten wie in G liefert,
I
bei dem jede Kante von G unabhängig mit Wahrscheinlichkeit p zu
G 0 hinzugenommen wird.
69 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Lemma
I
Wenn die Kanten eines Graphen G nach aufsteigendem Gewicht
sortiert vorliegen,
I
dann kann zu gegebenen p ein MSF F 0 für ein
G 0 = RandomSample(G, p) konstruiert werden,
I
indem man jede Kante von G nur einmal betrachtet.
Achtung:
I
Wir werden dieses Vorgehen nicht in unserem letzendlichen
Algorithmus verwenden,
I
sondern nur, um das Lemma nach diesem zu beweisen.
70 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis
Kanten e1, . . . , em nach aufsteigendem Gewicht geordnet
I konstruiere gleichzeitig
G 0 = RandomSample(G, p) und MSF F 0 von G 0
F00 ← ∅; k ← 0
for i ← 1 to m do
h„betrachte“ Kante ei i
if RandomFloat(0, 1) ≤ p then
hnimm ei = {u, v} zu G 0 hinzui
I
lautes Nachdenken an der Tafel
fi
fi
od
71 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis
Kanten e1, . . . , em nach aufsteigendem Gewicht geordnet
I konstruiere gleichzeitig
G 0 = RandomSample(G, p) und MSF F 0 von G 0
F00 ← ∅; k ← 0
for i ← 1 to m do
h„betrachte“ Kante ei i
if RandomFloat(0, 1) ≤ p then
hnimm ei = {u, v} zu G 0 hinzui
0 i then
if hu, v in versch. Zshg.komp. von Fk−1
k ← k + 1; Fk0 ← Fk0 −1 + ei
fi
fi
od
F 0 ← Fk0 hist der MSF i
I
71 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis (2)
I
Offensichtlich wird ein Wald F 0 konstruiert.
I
zeige: F 0 ist MSF (mit vorigem Lemma)
I
zeige: jede F 0-leichte Kante von G 0 ist in F 0.
I
Annahme: e= {v1, v2 } ist F 0-leichte Kante von G 0, die nicht in F 0 ist.
Zwei Möglichkeiten:
I
1. v1 und v2 liegen in verschiedenen Bäumen von F 0.
2. v1 und v2 liegen in einem Baum T 0 von F 0, eine Kante e 0
auf Pfad v1 ; v2 in T hat größeres Gewicht als e
72 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis (2)
I
Offensichtlich wird ein Wald F 0 konstruiert.
I
zeige: F 0 ist MSF (mit vorigem Lemma)
I
zeige: jede F 0-leichte Kante von G 0 ist in F 0.
I
Annahme: e= {v1, v2 } ist F 0-leichte Kante von G 0, die nicht in F 0 ist.
Zwei Möglichkeiten:
I
I
1. v1 und v2 liegen in verschiedenen Bäumen von F 0.
2. v1 und v2 liegen in einem Baum T 0 von F 0, eine Kante e 0
auf Pfad v1 ; v2 in T hat größeres Gewicht als e
in beiden Fällen galt, als e betrachtet wurde und ein Fk0 vorlag:
I
I
v1 und v2 lagen in verschiedenen Bäumen von Fk0 .
Dann wäre aber e zu Fk0 hinzugenommen worden.
72 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Lemma
I
Sei F 0 der MSF von G 0 = RandomSample(G, p).
I
Dann ist der Erwartungswert für die Anzahl der F 0-leichten Kanten
von G (!) kleiner oder gleich n/p.
73 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis (1)
I
I
betrachte vorangegangenen Algorithmus
Wenn Kante e von G am Ende
I
I
F 0-leicht ist, dann war sie auch schon Fk0 -leicht zu dem Zeitpunkt,
zu dem sie „betrachtet“ wurde
F 0-schwer ist, dann war sie auch schon Fk0 -schwer zu dem
Zeitpunkt, zu dem sie „betrachtet“ wurde
74 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis (2)
I
Phase i ≥ 1: Schleifendurchläufe solange k = i − 1
I
0 -leicht ist,
Während Phase i hat jede Kante von G, die Fi−1
0 hinzu
Wahrscheinlichkeit p, dass sie zu G 0 und folglich zu Fi−1
genommen wird.
I
mit erster Wahl einer solchen Kante endet die Phase
I
0 -leichten Kanten
Anzahl der in Phase i betrachteten Fi−1
geometrisch verteilt mit Parameter p
I
Erwartungswert ist 1/p
75 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis (3)
I
Am Ende ist |F 0 | = k ≤ n − 1, d. h. es ist k ≤ n − 1 mal die
Bedingung RandomFloat(0, 1) < p erfüllt.
I
Berücksichtigung der restlichen F 0-leichten Kanten,
die alle nicht mehr zu F 0 hinzugenommen werden:
I
I
I
for-Schleife weitermachen, bis n mal Bedingung erfüllt
Erwartungswert für Anzahl Schritte jeweils 1/p bis einmal der Fall
ZV Y : insgesamt notwendige Schleifendurchläufe
I
Y dominiert interessierende Anzahl Schleifendurchläufe.
I
E[Y ] = n/p.
76 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Randomisierter Algorithmus für MSF-Berechnung
1.
2.
3.
4.
5.
6.
proc F ← MSF(G):
G 1 ← B(B(B(G)))
C1 ← hKanten, die bei Berechnung von G 1 kontrahierti
if hG 1 enthält keine Kanten mehri then
return C1
fi
G 2 ← RandomSample(G 1, 1/2)
F2 ← MSF(G 2 )
C2 ← hdie F2-schweren Kanten in G 1 i
G 3 ← hG 1 ohne die Kanten in C2 i
F3 ← MSF(G 3 )
F ← C1 ∪ F3
return F
77 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Satz
Der obige Algorithmus berechnet den MSF des Eingabegraphen G.
78 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis
zu 1. Die Kanten aus C1 gehören zum MSF von G.
Enthält G 1 keine Kanten, dann bildet Kantenmenge C1 den MSF.
zu 3. F2 ist ein Wald in G 2 und folglich auch in G 1 und G.
zu 4. Die F2-schweren Kanten von G 1 gehören nicht zum MSF von G 1.
Folglich hat G 3 den gleichen MSF wie G 1,
zu 5. der als F3 berechnet wird.
zu 6. Also ist C1 ∪ F3 ein MSF und wegen Zusammenhang sogar ein
MST von G.
79 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Satz
Der Erwartungswert für die Laufzeit des Algorithmus ist O(m + n).
80 / 81
Graph-Algorithmen
Minimale aufspannende Bäume
Ein randomisierter MSF-Algorithmus
Beweis
T (n, m): Erwartungswert der Laufzeit des Algorithmus für Graphen mit
n Knoten und m Kanten.
1. G 1 ← B(B(B(G))): Laufzeit ist O(m + n).
G 1 hat höchstens n/8 Knoten und m Kanten.
2. G 2 ← RandomSample(G 1, 1/2): Laufzeit ist O(m + n).
G 2 hat ≤ n/8 Knoten und erwartete Kantenzahl m/2.
3. F2 ← MSF(G 2 ): erwartete Laufzeit ist T (n/8, m/2)
4. C2 ← hdie F2-schweren Kanten in G 1 i: Laufzeit ist O(m + n).
G 3 hat ≤ n/8 Knoten; erwartete Kantenzahl (n/8)/(1/2) = n/4.
5. F3 ← MSF(G 3 ): erwartete Laufzeit T (n/8, n/4)
6. F ← C1 ∪ F3: Laufzeit ist O(n).
T (n, m) ≤ T (n/8, m/2) + T (n/8, n/4) + c(n + m) .
; T (n, m) ∈ O(n + m).
81 / 81