appendix

Zusatz Formelsammlung Technische Mechanik
Stefan Rickli, ricklis@student.ethz.ch
APPENDIX
Bei einer Torsion:
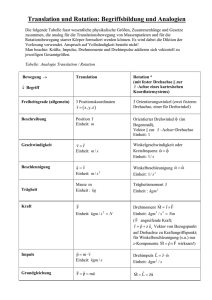
1 Mechanik allgemein
𝑀 = −𝐷𝜑
1.1 Planare Bewegungen
D: Direktionsmoment (siehe 1.3.1) / Federkonstante
G: Schubmodul (siehe S.Error! Bookmark not defined.)
1.1.1 Impuls
𝑝⃗ = 𝑚𝑣⃗
[𝑝] = Ns
1.1.2 Kraft
1.2.4 Trägheitsmoment ≅ Masse
ⅆ𝑝⃗
𝐹⃗ = ma⃗⃗ =
= 𝑝⃗̇
ⅆ𝑡
1.1.3 Trägheitskraft
kgm
[𝐹] = N = 2
s
D’Alembertsche Trägheitskraft:
𝐹 = 𝑚𝑎 ⇔ 𝐹 − 𝑚𝑎 = 0
⇒ 𝐹 − 𝐹𝑇 = 0
1.2 Drehbewegungen
1.2.1 Winkel
Massenträgheitsmoment, Inertialmoment, Moment of inertia;
Widerstand eines starren Körpers gegenüber einer Änderung
seiner Rotationsbewegung um eine gegebene Achse.
⃗⃗⃗ = 𝐼𝜔
𝑀
⃗⃗̇
[𝐼] = kg m2
vergl. 𝐹⃗ = 𝑚𝑎⃗
Allgemeine Definition:
𝛼=
𝑑𝜔
𝑑𝜑
= 𝜔̇ , 𝜔 =
= 𝜑̇
𝑑𝑡
𝑑𝑡
𝐼 = ∫ 𝑟⃗⊥2 𝜌(𝑟⃗) 𝑑𝑉
𝑉
1.2.2 Drehimpuls ≅ Impuls, Energie
𝑟⃗⊥ : der zur Rotationsachse 𝜔
⃗⃗ (Winkelgeschwindigkeit)
senkrechte Anteil von 𝑟⃗ (also quasi Abstand zur Achse).
𝜌(𝑟⃗): ortsabhängige Dichte. Bei konstanter Dichte kann diese
auch vor das Integral gezogen werden.
Angular Momentum; Drall, Impulsmoment, Schwung der
Drehung
Einige Trägheitsmomente:
ϕ: Drehwinkel, ω: Winkelgeschwindigkeit,
α: Winkelbeschleunigung
Dünner Stab, Drehachse in der Mitte: 𝐼 =
Drehimpuls eines Massepunktes:
𝐿⃗⃗ = 𝑟⃗ × 𝑝⃗
1
[𝐿] = Nms
1
𝑚ℓ2
12
2
Dünner Stab, Drehachse am Ende: 𝐼 = 𝑚ℓ
3
1
Massiver Zylinder, Drehachse längs: 𝐼 = 𝑚𝑟 2
2
𝑟⃗: Ortsvektor des Massepunktes
p: Impuls des Massepunktes 𝑝⃗ = 𝑚𝑣⃗
L ist in trivialen Fällen parallel zu Drehachse.
Vollkugel: 𝐼 ≅ 𝑚𝑟 2
Rotation eines starren Körpers um eine Symmetrieachse:
Bezugsachsenwechsel: Satz von Steiner:
2
5
2
Hohlkugel mit Wandstärke 𝑑 ≪ 𝑟 : 𝐼 = 𝑚𝑟 2
3
𝐼2 = 𝐼1 + 𝑚𝑑 2
𝐿⃗⃗ = 𝐼𝜔
⃗⃗ = 𝐼𝜑
⃗⃗̇
I: Trägheitsmoment des st. Körpers
ω: Kreisfrequenz der Drehung
wobei d den Abstand der neuen zur alten parallelen,
Bezugsachse bezeichnet.
Massepunktwechsel:
1.3 Objekte
𝐿⃗⃗′ = 𝐿⃗⃗ + 𝑎⃗ × 𝑝⃗
1.3.1 Drehmoment eines verdrehten Vollkörpers
𝑎⃗: Vektor vom alten zum neuen Massepunkt
𝑝⃗: Impuls des neuen Massepunkts
𝑀=
allgemein evtl. mit Hohlraum:
1.2.3 Drehmoment ≅ Kraft
Torque;
𝑀 = 2𝜋
Änderungsrate des Drehimpulses
ⅆ𝐿⃗⃗
⃗⃗⃗ = r⃗ × 𝐹⃗ =
𝑀
= 𝐿⃗⃗̇
ⅆ𝑡
𝜋 𝜃𝐺𝑅4
2 𝐿
𝐺𝜃 𝑅 3
∫ 𝜌 𝑑𝜌
𝐿 𝑟
G: Schubmodul, θ: Drehwinkel, L: Länge, R/ρ: Radius
[𝑀] = Nm
L: Drehimpuls
Bei Drehung um eine feste Achse:
⃗⃗⃗ = 𝐿⃗⃗̇ = 𝐼𝜔
𝑀
⃗⃗̇ = 𝐼𝛼⃗
𝜔
⃗⃗̇ = 𝛼⃗ = Winkelbeschleunigung
zuletzt gespeichert: 08.04.2017 05:47:00, Version 4
1.3.2 Feder
𝐸𝐴
𝐹𝐹 = − ( ) ⋅ Δℓ = −𝑘𝑥
ℓ
FF = -FN
FF
also mit den Konstanten:
𝑘=
𝐸𝐴 𝐹
= ,
ℓ
ℓ
𝑥 = Δℓ
FN
1/4
Zusatz Formelsammlung Technische Mechanik
Ersatzfederkonstante bei mehreren Federn:
Parallelschaltung:
𝑘tot = ∑ 𝑘𝑖
𝑖
Serienschaltung:
1
1
=∑
𝑘tot
𝑘𝑖
𝑖
Potenzielle Energie einer Feder
1
𝐸𝑝𝑜𝑡 = 𝑘𝑥 2
2
Stefan Rickli, ricklis@student.ethz.ch
Vorgehen bei ebener Kinematik:
1. Welche SK sind miteinander verbunden, welche
unabhängig?
2. Markiere alle SK (verwende Farben, Schraffuren, etc)
3. Zeichne alle möglichen Geschwindigkeiten ein und
deren Wirkungslinien. Vergiss nicht: Scharniere sind
zwingendermassen ein Momentazentrum und Rollen
können sich nur auf einer Linie hin- und herbewegen.
4. Finde die Kreuzungen der Senkrechten zur
Geschwindigkeit bzw. bestimme die
Momentanzentren der jeweiligen SK.
5. Bestimme die Richtungen und Beträge der
Geschwindigkeiten (Verwende: Hände für die
Drehrichtung, SdpG und auch 𝑣𝑝 = 𝜔 ⋅ 𝑟𝑝 )
4 Kräfte und Momente
Lagerkräfte / -reaktionen bestimmen:
 SK / Fachwerk als Ganzes freischneiden und KB / MB
formulieren.
2 Diverses
Kleinwinkelapproximation:
cos 𝑥 ≅ 1
sin 𝑥 ≅ tan
⏟𝑥
gut für
≅𝑥
ⅆ
ⅆ𝑥
für kleine Winkel x.
3 Kinematik:




sobald zwei Geschwindigkeiten eines SK bekannt sind,
ist dessen Bewegungszustand eindeutig bekannt.
o Es lässt sich die Kinemate bestimmen.
{𝑣
⃗⃗⃗⃗⃗,
⃗⃗}
𝐵 𝜔
die Geschwindigkeit eines Punktes, der zwei SK durch
ein kugeliges Gelenk miteinander verbindet, gilt für
beide SK. Das heisst, man kann die Starrkörperformel
auf diesen Punkt jeweils von beiden SK aus berechnen
und gleichsetzen.
o Vorsicht mit den Einheiten!
𝑣
𝑣 =𝜔⋅ℓ⇔ 𝜔 =
ℓ
SdpG:
o funktioniert sowohl im 2D- als auch im 3DFall
o ⃗⃗⃗⃗⃗
𝑣𝑎 ⋅ ⃗⃗⃗⃗⃗⃗
𝐴𝐵 = ⃗⃗⃗⃗⃗
𝑣𝑏 ⋅ ⃗⃗⃗⃗⃗⃗
𝐴𝐵
Momentanzentren:
o im 3D lassen sich Momentanzentren nur bei
festen Kugelgelenken direkt bestimmen.
Deren SK können dann nur Rotationen
ausführen.
o im 2D befindet sich das MZ eines SK im
Schnittpunkt der Senkrechten zu den
Geschwindigkeiten der Punkte auf dem SK.
zuletzt gespeichert: 08.04.2017 05:47:00, Version 4
Statisch äquivalente Kräfte finden:
Resultierende und Moment müssen in einem beliebigen Punkt
verschwinden. D.h. es muss gelten
⃗⃗⃗⃗⃗⃗⃗
𝐹𝑆𝐴 = 𝑅⃗⃗
Angriffspunkt der statisch äquivalenten Kraft:
Man greift zum Momentengleichgewicht:
⃗⃗⃗⃗⃗⃗
𝑀𝑃 = (𝑟⃗⃗⃗𝑠 − ⃗⃗⃗⃗)
𝑟𝑃 × ⃗⃗⃗⃗
𝐹𝑠 ,
wobei P irgendein Punkt auf dem Starrkörper sein kann und ⃗⃗⃗⃗
𝑟𝑃
ist der unbekannte Ortsvektor des Angriffspunktes
(Verbindungsvektor!).
Statisch äquivalentes Moment finden:
⃗⃗⃗⃗⃗⃗
𝑀𝑃 = ⃗⃗⃗⃗⃗⃗⃗⃗
𝑀𝑆𝐴
Der Angriffspunkt muss hier P sein.
5 Leistung und Stabkraft
Stabkraft in Fachwerk bestimmen / PdvL in Fachwerk:
1. Stab entfernen, durch Zugkraft ersetzen
2. einem SK eine möglichst geschickte Rotation
verpassen
3. alle Geschwindigkeiten an den Kraftangriffspunkten
bestimmen
4. Leistungen aufsummieren, gleich Null setzen
a. ein an einem SK angreifendes Moment
einfach mit dessen Winkelgeschwindigkeit
multiplizieren
b. Vorzeichen ergeben sich durch die
Skalarprodukte von Geschwindigkeit mit
Kraft
(𝑎 ⋅ 𝑏 ⋅ cos 𝜑 , 𝑎⃗ ⋅ 𝑏⃗⃗)
Wenn Lagerkräfte bereits duch vorherige Berechnungen
bekannt sind, vereinfacht sich die Berechnung mit dem PdvL
eventuell wesentlich, weil ein weniger SK involvierender
Bewegungszustand gewählt werden kann.
2/4
Zusatz Formelsammlung Technische Mechanik
Stefan Rickli, ricklis@student.ethz.ch
6 Dynamik
Dynamik Vorgehen:
1. Bestimme jene Körper mit Masse, von welchen die
Dynamik beschrieben werden muss
2. Führe geeignete Koordinaten ein, welche die
Bewegung der Körper eindeutig beschreibt
3. Schneide die Körper, falls nötig, an den relevanten
Stellen frei
4. Stelle die dynamischen Gleichungen auf: 𝑚𝑥̈ =
⋯ , 𝐼𝜑̈ = ⋯
5. Falls der Freiheitsgrad des Systems kleiner als die
Anzahl der eingeführten Koordinaten ist: finde
Bindungsgleichungen an den Verbindungsstellen
(kinematische Relationen).
6. Eliminiere Kräfte vom Freischnitt (z.B. Federkräfte –
auf richtiges Vorzeichen in DGL aufpassen)
7. Zusammenfassen der DGL
8. Aufstellen der Anfangsbedingungen
9. Lösen der DGL
8 Bindungskräfte
7 Diverses
Hinweise:






Rolle ideal rau: nur T / Fhaft einführen, aber keine
Bedingung an μ.
kinematische Relationen: Zusammenhänge zwischen
allen fix verhängten Koordinatensystemen und deren
Variablen
Flaschenzug: lässt sich mit Momentenbedingungen
rasch abhandeln. Relevant sind nur ausgewählte
Komponentenbedingungen, z.B. jene beim
Verbundstück
Wenn zwei Punkte desselben SK die gleiche
Geschwindigkeitsrichtung haben, so muss gelten:
o die Beträge sind gleich (SdpG)
o der momentane Bewegungszustand dieses SK
ist eine Translation
Statisch bestimmt: nicht mehr Variablen wie
Gleichungen
Kinematisch unbestimmt: zulässige Bewegung möglich
zuletzt gespeichert: 08.04.2017 05:47:00, Version 4
3/4
Zusatz Formelsammlung Technische Mechanik
Stefan Rickli, ricklis@student.ethz.ch
9 Schwerpunkte
Schwerpunkt berechnen:
𝑟𝑠 =
⃗⃗⃗
1
∑ 𝑚𝑖 ⋅ ⃗⃗⃗⃗
𝑟𝑠𝑖
𝑚𝑡𝑜𝑡
𝑖
Gesamtschwerpunkt ist Umkehrwert der Gesamtmasse mal
(Summe der nach Teilmasse gewichteten Schwerpunkte der
geometrisch einfacheren Teilkonstrukte)
Manchmal lohnt es sich auch, zu einem grossen, einfachen
Objekt den Schwerpunkt eines anderen abzuziehen.
zuletzt gespeichert: 08.04.2017 05:47:00, Version 4
4/4