Grundlagen der Computertechnik

Grundlagen der Computertechnik
Aufbau von Computersystemen und Grundlagen des Rechnens
Walter Haas
PROLOG WS2012
Automation Systems Group E183-1
Institute of Computer Aided Automation
Vienna University of Technology
email: tgi@auto.tuwien.ac.at
Grundfragen
Auf der Suche nach dem Grundbaustein der Information
2
Was ist Information?

Information ist Information
 Information ist weder Materie noch Energie

Informationsmenge
 „Erkenntnisinteresse“ des Empfängers
 „Überraschungswert“ einer Nachricht
 Beseitigen oder Verkleinern von Ungewissheit

Klassische Informationstheorie
Claude E. Shannon (1916-2001)
A Mathematical Theory of
Communication
 Shannon (1948), Untersuchungen zum Informationstransport über
einen Nachrichtenkanal
 Informationsgehalt eines Zeichens
 Wahrscheinlichkeit für das Auftreten des Zeichens in einer Nachricht
 Folge unabhängiger Zeichen
 Informationssumme der Einzelzeichen => Informationsgehalt der Nachricht
3
Wie kann man Information messen ?

Entscheidung zwischen zwei Alternativen
 Einfachste Grundsituation im Informationsaustausch
 Per Definition Grundeinheit der Information

Bit („Binary Digit“)
 1 Bit entspricht dem Informationsgehalt einer



Entscheidung zwischen 2 Alternativen
(„Ja-Nein-Entscheidung“).
Jede Information ist als Folge von „binären“
Entscheidungen darstellbar
Jedes zusätzliche Bit Information verdoppelt
John W. Tukey (1915-2000)
die Anzahl der Alternativen.
Synonyme Zuordnungen:
1 - 0, Ja - Nein, Ein - Aus, Wahr - Falsch, High - Low, …
4
Technik der Informationsdarstellung

Notwendig: Eindeutig unterscheidbare Zustände
 Mit 2 Zuständen einfach realisierbar!
Relais
Transistor
ElektronenRöhre
Schalter
Lochstreifen
Lochkarte
Ringkernspeicher
Strich-Code
5
Schaltalgebra
Logik als Basis der Computerkonstruktion
6
Boolesche Algebra

„Algebra der Logik“ (1847)
 Grundlage, um Logik formal auszudrücken

Operationen mit „Aussagevariablen“
 Aussagevariablen, Platzhalter für log. Aussagen
 Variable mit wahr oder falsch belegt.
 „Zweierschritt“ => 1 Bit Information

George Boole (1815-1865)
Weiterentwicklung durch Shannon (1938) => „Schaltalgebra“
 Mathematische Behandlung komplexer elektrischer Systeme
 Schaltungen aus Relais und Schaltkontakten
 Struktur dargestellt durch mathematische Gleichungen
7
Logische Grundfunktionen
Ein einfaches Modell für Aussagevariablen:
Ventil / Schalter A in der linken Stellung
• Aussage A ist wahr
• Wasser / Strom fließt
A=1
Logische Funktionen können durch Verknüpfen
mehrerer Aussagevariablen gebildet werden!
Ventil / Schalter A in der rechten Stellung
• Aussage A ist falsch
• Wasser / Strom gesperrt.
A=0
8
Möglichkeit 1: Serienschaltung
Gesamtaussage ist WAHR (1),
wenn A UND B WAHR (1) sind!
A B
Wahrheitstabelle
A B AB
1
1
0
0
1
0
1
0
1
0
0
0
9
Möglichkeit 2: Parallelschaltung
Gesamtaussage ist WAHR (1),
wenn A ODER B WAHR (1) ist
oder beide WAHR (1) sind!
A B
Wahrheitstabelle
A B AB
1
1
0
0
1
0
1
0
1
1
1
0
10
Möglichkeit 3: Negation
Aussage NICHT A ist WAHR (1)
wenn A FALSCH (0) ist!
A
Wahrheitstabelle
A ¬A
1
0
0
1
11
Beispiel: Gasthaus „Zum Scharfen Eck“

4 Kriterien müssen erfüllt sein, damit
ein Gast willkommen ist:
 Der Gast ist nicht betrunken ¬ A
 Der Gast ist hungrig B  C

oder durstig
Der Gast zahlt bar D
Wahrheitstafel
A B C D ¬ A BC ¬A(BC)D
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
12
Rechenregeln der Booleschen Algebra

Assoziativgesetz
 (A  B)  C = A  (B  C)

Kommutativgesetz
 AB=BA

AB=BA
Distributivgesetz
 A  (B  C) = (A  B)  (A  C)

(A  B)  C = A  (B  C)
A  (B  C) = (A  B)  (A  C)
Weitere Umformungsregeln




A0=0
A1=A
AA=A
A  ¬A = 0
A0=A
A1=1
AA=A
A  ¬A = 1
13
Berechnen der Schaltung aus der Wahrheitstafel

1. Schritt: „Auslesen“ der 1en…
(¬A  B  C  D)  (¬A  B  ¬C  D)  (¬A  ¬B  C  D)

2. Schritt: Distributivgesetz
¬A  [(B  C)  (B  ¬C)  (¬B  C)]  D

3. Schritt: Assoziativ- und Distributivgesetz
¬A  {[B  (C  ¬ C)]  (¬B  C)]  D

4. Schritt: A  ¬A = 1
¬A  {[B  1]  (¬B  C)}  D

5. Schritt: A  1 = A
¬A  [B  (¬B  C)]  D

6. Schritt: Distributivgesetz + Vereinfachen
¬A  [(B  ¬B)  (B  C)]  D

7. Schritt: A  ¬A = 1 und A  1 = A
¬A  (B  C)  D
A BCD
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
F(A,B,C,D)
0
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
14
Bauelemente

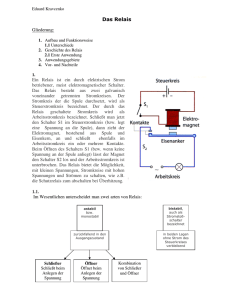
Relais
 Zuse Z3 (1941) ca. 2000 Relais
 Harvard Mark II (1947)
15
Bauelemente

Relais
 Zuse Z3 (1941) ca. 2000 Relais
 Harvard Mark II (1947)

Elektronenröhre
 Colossus (1943), ca. 2500 Röhren
 ENIAC (1946)
ca. 17 000 Röhren, 7000 Dioden, 1500 Relais
16
Bauelemente

Relais
 Zuse Z3 (1941) ca. 2000 Relais
 Harvard Mark II (1947)

Elektronenröhre
 Colossus (1943), ca. 2500 Röhren
 ENIAC (1946)
ca. 17 000 Röhren, 7000 Dioden, 1500 Relais

Transistor
 TRADIC (1955)
ca. 700 Transistoren, 10 000 Dioden
 Mailüfterl (1958),
ca. 3000 Transistoren, 5000 Dioden
0
nicht
leitend
leitend
1
17
Bauelemente

Relais
 Zuse Z3 (1941) ca. 2000 Relais
 Harvard Mark II (1947)

Elektronenröhre
 Colossus (1943), ca. 2500 Röhren
 ENIAC (1946)
ca. 17 000 Röhren, 7000 Dioden, 1500 Relais

Transistor
 TRADIC (1955)
ca. 700 Transistoren, 10 000 Dioden
 Mailüfterl (1958),
ca. 3000 Transistoren, 5000 Dioden

Integrierte Schaltungen (ab 1961)
 IBM/360 Serie (ab 1964)
 Mikroprozessoren
 Intel 4004 (1971)
ca. 2300 Transistoren
 Texas Instruments TMS1000 (1974)
18
Schaltsymbole (1)

Logikgatter – Logische Grundfunktionen als Bauteile
 Beispiel: UND-Funktion
Eingänge
0 oder 1
&
Ausgang der
Gesamtschaltung:
• 0 (nicht leitend)
• 1 (leitend)
19
Schaltsymbole (2)

Grundfunktionen
 Negation (NOT-Gate)
 Konjunktion (AND-Gate)
A
A
1
&
AB
≥1
AB
=1
AB
B
 Disjunktion (OR-Gate)
A
B

¬A
Exklusives ODER (XOR):
A B AB
1
1
0
0
1
0
1
0
0
1
1
0
A
B
A  B = (A  ¬B)  (¬A  B)
20
Schaltsymbole (3)

Zutrittsfunktion „Zum Scharfen Eck“…
A

…als Gatterschaltung
realisiert
B
1
≥1
&
C
D
21
Wurzeln des Rechnens
Zahlensysteme und Rechenschaltungen
22
Dezimalsystem

Positionssystem (Stellenwertsystem)
 Wertigkeit einer Ziffer abhängig von der Position



innerhalb der Zahl
Wertigkeiten sind Vielfache der Basis 10
Zeichenvorrat (Ziffernzeichen) 0, 1,…, 9
Sonderstellung der Ziffer 0
 „...gilt allein nichts, außer wenn sie anderen Ziffern
nachgesetzt wird, so erhöht sie deren Wert…“
Beispiel:
zehntel
hundertstel
7 8 9 5.3 1
tausend
hundert
zehn
eins

Adam Ries (1492 - 1559)
=
+
+
+
+
+
7 x 1000
8 x 100
9 x 10
5x1
3 x 1/10
1 x 1/100
(103)
(102)
(101)
(100)
(10-1)
(10-2)
23
Alternative Zahlensysteme (1)
„Die ganzen Zahlen hat der liebe Gott geschaffen,
alles andere ist Menschenwerk.“

Art und Weise des Zählens
 Zahlendarstellung => Künstlich geschaffenes System
 In unabhängigen Kulturen unabhängig entwickelt
Leopold Kronecker
(1823 - 1891)


Zählen im Dezimalsystem
 Historisch gewachsen
 Wahl der Basis 10 ist willkürlich
„Zahl“ ist nur eine Abstraktion für eine „Anzahl von Dingen“
Rechnen = Zusammenrechen
24
Alternative Zahlensysteme (2)

Allgemeines Positionssystem mit Basis b > 1
 Ziffernzeichen ai : 0 ... (b-1)
 (... a3 a2 a1 a0  a-1 ...)b = ... + a3 b3 + a2 b2 + a1 b1 + a0 b0 + a-1 b-1 + ...

Binärsystem (Basis b = 2)
 2 Ziffernzeichen: 0 und 1
 Beispiel:
(1010.1)2 = 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 + 1 x 2-1

Hexadezimalsystem (Basis b = 16)
 16 Ziffernzeichen: 0 ... 9, A ... F
Gottfried Wilhelm Leibniz
(1646 - 1716)
 Beispiel:
(A9.E)16 = 10 x 161 + 9 x 160 + 14 x 16-1
25
Rechnen im Binärsystem

Rechenvorschriften analog zum Dezimalsystem
 Stellenweise, rechts beginnen, bei Bedarf Übertrag auf nächste Stelle

Addition





0+0=0
1+0=1
0+1=1
1 + 1 = 10 Übertrag 1
11011
1010
1 1 0 1 0
Übertrag
100101
Subtraktion
 0 -0=0
 1 -0=1
 10 - 1 = 1, Übertrag 1
 1 -1=0
10001
- 1010
1 1 1 0
Übertrag
00111
26
Konstruktion eines Addierers für Binärzahlen
Logische Schaltung zum Addieren einer Stelle zweier Binärzahlen
 Eingänge ai und bi für die Summanden
 Ausgang für die Summe si
 Ausgang für den Übertrag ci

bi
+

ai
si
ci
Übertragen der Rechenregeln in eine Wahrheitstabelle




0+0=0
1+0=1
0+1=1
1 + 1 = 10 Übertrag 1
ai bi si ci
0
1
0
1
0
0
1
1
0
1
1
0
0
0
0
1
27
Konstruktion eines Addierers für Binärzahlen (2)

Auslesen der 1en aus der Wahrheitstabelle
ai bi si ci
 si = (ai  ¬bi)  (¬ai  bi) = ai  bi
 ci = ai  bi

0
1
0
1
0
0
1
1
0
1
1
0
0
0
0
1
Fertige Addier-Schaltung
ai
bi
si
ci
28
Addition mehrstelliger Binärzahlen

Problem: Was passiert mit Übertrag ci-1?
ai bi
HA
ai bi ci-1
ci-1
bi
ai
ci si
„Halbaddierer“

HA
HA
s‘
c‘
si
≥1
ci
VA
ci
si
„Volladdierer“
Beispiel:
4 Bit Addierer
29
Zahlendarstellungen
Grundlagen der Computerarithmetik
30
Die Welt der Zahlen
Negative
Zahlen?
-1, -2,…
, ,…
Rationale
Die Welt besteht
Zahlen?
nicht nur aus
positiven ganzen
Wie lassen sich
Zahlen!!!
Reelle
Zahlen?
,
solche Zahlen in
einem Computer mit
„0“ und „1“
darstellen?
31
Negative Zahlen

Wie lassen sich positive und negative Zahlen unterscheiden?
Vorzeichen:
+ 11 7
- 11 7
+ positiv
- negativ
Vorzeichen
Betrag
Darstellung in 0 und 1

Idee: Reservieren 1 Bit mit fester Position für Vorzeichen!
(1110101)2 = (117)10
• 0 => positiv (+)
• 1 => negativ (-)
1 1 1 1 0 1 0 1
= (-117)10
Feste Wortlänge (!)
32
Darstellung mit Vorzeichen und Betrag

Zahlenkreis
1111
15
-7
1110
Positive
Zahlen
0000
0
0001
1
2
-6
14
1101
3 0011
-5
13
-4
1100 12
4
Negative
Zahlen
0100
5 0101
-3
1011 11
1010
0010
-2
10
6
9-1
1001
-0
8
1000
7
0110
0111
33
Einerkomplement

Positive Zahlen
 Betrag als Dualzahl
1111
-0
1110

Negative Zahlen
 Invertieren der


Bits des Betrags
0 => 1
1 => 0
0000
0
0001
1
2
-1
1101
3 0011
-2
1100 -3
4
0 1 0 1 = (5)10
1010
0100
5 0101
1011 -4
Beispiel:
0010
6
-5
-6
1001
-7
1000
7
0110
0111
1 0 1 0 = (-5)10
34
Zweierkomplement

Positive Zahlen
 Betrag als Dualzahl
1111

Negative Zahlen
 Einerkomplement + 1
0
0001
1
2
-2
1101
Beispiel:
-1
1110
0000
0010
3 0011
-3
1100 -4
4
0100
0 1 0 1 = (5)10
5 0101
1011 -5
1010
+0001
Einerkomplement
1 0 1 1 = (-5)10
1010
6
-6
-7
1001
-8
1000
7
0110
0111
35
Rechnen im Zweierkomplement

Vorteil der Zweierkomplementdarstellung:
 Algebraische Vorzeichenregeln ergeben sich auf natürliche Weise!
 Keine separate Subtraktion notwendig.

Beispiel: (7)10 – (4)10 (4 Bit Darstellung)
1.Schritt: Zweierkomplement
(4)10 = (0100)2
0100
Einerkomplement
1011
+0 0 0 1
1100
= (-4)10
2.Schritt: Addition
0111
+ 1100
1 1 0 0
Übertrag
0011
Führende 1 durch begrenzte
Wortbreite verloren
36
Rationale und Reelle Zahlen

Numerische Berechnungen
 Oft sind Berechnungen mit „gebrochenen“ Zahlen notwendig
 Erforderlich => Darstellung reeller Zahlen in Computern

Naheliegende Idee: „Festpunkt-Zahlensystem“
 Feste Unterteilung der Stellen
 Vorkommastellen
 Nachkommastellen
 Vorzeichen (0 ⇒positiv, 1 ⇒negativ)
 Gesamtlänge
VZ
1
Bit
Vorkommateil (g)
Nachkommateil (n)
„Binärpunkt“ oder „Dezimalpunkt“
37
Vorteile-/Nachteile der Festpunktdarstellung

Vorteile
 Für den Menschen leicht verständlich
 Addition/Subtraktion einfach
 Multiplikation/Division mit Skalierungsfaktor möglich

Nachteile




Intervall zwischen größter und kleinster darstellbarer Zahl klein
Position des Binärpunktes fix
Keine flexible Aufteilung zwischen Vorkomma-/Nachkommateil
Wünschenswert:
 Große Zahlen mit wenigen Nachkommastellen
 Kleine Zahlen mit vielen Nachkommastellen

Lösung: Gleitpunkt-Darstellung
38
Gleitpunktdarstellung (1)

Grundidee
 Jede Zahl erhält einen individuellen Skalierungsfaktor
 Wahl des Skalierungsfaktors: bk (abhängig von Basis b)
 bk entspricht Verschieben des Binär-/Dezimalpunktes um k Stellen

Anpassung der Genauigkeit an Größenordnung der Zahl
 Große Zahlen, weniger Nachkommastellen
 Kleine Zahlen, mehr Nachkommastellen
Beispiele (dezimal):
123 10
123000000000
123 10
0.000000123
39
Gleitpunktdarstellung (2)

Mehrdeutigkeit der Darstellung
 Mit verschiedenen Skalierungsfaktoren mehrere Darstellungen für die
selbe Zahl
Beispiel (dezimal):
123 10
12.3 10
0.123
10
123000000000

Lösung: Normalisierte Form der Darstellung
 Eingeschränkte Wahl der Skalierung
 Position des Binärpunktes so, dass erste Ziffer immer ungleich 0 !
Beispiele (dezimal):
1.23 10
123000000000
1.23 10
0.000000123
40
Codierung einer Binären Gleitpunktzahl

Reserviere in einer Folge von Binärziffern Felder fester Länge für
 Vorzeichenbit (0 ⇒positiv, 1 ⇒ negativ)
 Exponent ohne Basis ( Stellen)
 Mantisse = Ziffern der Zahl Stellen)
VZ
Exponent
Mantisse
Indizierung
Bitnummer
msb
lsb
1
Bit
41
Rechnen mit Gleitpunktzahlen

Beispiel: Addition
 1.23 10 ≡ 123000
 2.00 10 ≡ 2000

Addition Schritt 1: Angleichen der Exponenten
 „Rechtsschieben“ der Zahl mit dem kleineren Exponenten
 1.23 10
 0.02 10

Addition Schritt 2: Addieren der Mantissen
 1.23 0.02

10
1.25
10
Addition Schritt 3: Normalisieren des Ergebnisses
 Wenn Vorkommateil 0 oder mehrstellig (>9) ist!
 Im Beispiel ist das Ergebnis bereits normalisiert.
42
Genauigkeit von Fließpunktzahlen (1)

Endliche Stellenanzahl der Computerzahlen
 Endlicher Vorrat an Fließpunktzahlen
 Die Zahlengerade weist Lücken auf
 Nur wenige Reelle Zahlen sind genau darstellbar!
-7

-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
Beschränkte Menge von Fließpunktzahlen
 Selbst einfache (Dezimal-)Zahlen lassen sich binär nicht genau angeben!
 Ergebnis einer Rechenoperation fällt nicht immer genau auf eine
darstellbare Fließpunktzahl.

Zahlen und Rechenergebnisse müssen gerundet werden
 Runden = Abbildung auf Menge der darstellbaren Fließpunktzahlen
 Konsequenz: Rechnungen sind mit Ungenauigkeiten behaftet!
43
Genauigkeit von Fließpunktzahlen (2)
Beispiel: Umwandeln von (0.1)10 ins Binärsystem

0.1 x 2 = 0.2
0
0.2 x 2 = 0.4
0
0.4 x 2 = 0.8
0
0.8 x 2 = 1.6
1
0.6 x 2 = 1.2
1
0.2 x 2 = 0.4
0
…
…
Ergebnis ist eine periodische
Binärzahl:
0.0001100110011001100110011…
Wie groß ist der Rundungsfehler?
 Angenommen: Nur 5 Nachkommastellen darstellbar, restliche Stellen


werden abgeschnitten
Rückrechnung: 0.00011
2
2
0.0625 0.03125
Absoluter Rundungsfehler: 0.1 0.09375 0.00625
0.09375
44
Auswirkung von Rundungsfehlern

Algebraische Gesetze teilweise nicht mehr gültig
 Assoziativgesetz: 1.23 0.0153 0.456 (Kaufm. Runden auf 3 Stellen)

1.23
0.0153
1.2453
1.25

0.0153
0.456
0.456
1.706
0.4713
0.471
0.471
1.701
1.23

1.25
1.71
1.70
Fehler pflanzen sich fort




Instabilitäten bei numerischen Berechnungen
Mangelnde Zuverlässigkeit von Ergebnissen
Extremfall: Auslöschungseffekt
Beispiel: 3.34 4 1.22 2.28(Kaufm. Runden auf 3 Stellen)




3.34
11.1556 11.2
4 1.22 2.28 11.1264 11.1
Ergebnis mit Rundungsfehler: 11.2
Exaktes Ergebnis: 0.0292
11.1
0.1
45
Zusammenfassung

Information
 Minimaler Informationsgehalt => Entscheidung zwischen 2 Alternativen
 Klassische Informationstheorie von Shannon
 1 Bit als kleinste Informationseinheit

Schaltalgebra
 Logik als Grundlage der Computerkonstruktion (Boolesche Algebra)
 Grundfunktionen: UND, ODER und Negation
 Ermöglicht Systematische Berechnung von Schaltfunktionen

Zahlensysteme





Unterscheidung Zahl und Zahlendarstellung
Positionssystem als verallgemeinerte Darstellung
Binäre Zahlendarstellung im Computer
Darstellung negativer Zahlen durch Zweierkomplement
Darstellung Reeller Zahlen durch Gleitpunktdarstellung
46
Quellenangaben

Charles Petzold
CODE, The Hidden Language of Computer Hardware and Software
Microsoft Press 2000

H. R. Wieland
Computergeschichte(n) – nicht nur für Geeks. Von Antikythera zur Cloud
Galileo Computing, 2011

Friedrich L. Bauer
Historische Notizen zur Informatik
Springer Verlag, 2009

Walter R. Fuchs
Knaurs Buch der Denkmaschinen
Droemer Knaur, 1968

David Goldberg
What Every Computer Scientist Should Know About Floating Point Arithmetic
ACM Computing Surveys, Vol. 23, No. 1, March 1991

WIKIPEDIA
www.wikipedia.org

Computer History Museum
www.computerhistory.org

The Antique Chip Collectors Page
www.antiquetech.com

The MacTutor History of Mathematics Archive
www.history.mcs.st-andrews.ac.uk

ORACLE ThinkQuest – Computer History
http://library.thinkquest.org/18268/History/
47